搜尋邏輯思考

在連連看裡面，連線的線條不可超過兩個轉彎處，兩個轉彎處的意思，代表連接的線最多只能由三條直線來組成。

這時候我們來思考該如何找出這兩點間所存在的那條線。先觀察一下棋盤，最多三條直線，代表有可能是一條直線、兩條直線或三條直線來做連接的。

不論如何，兩個點之間的那條線，一定一邊是從第一個點(A)開始，到另一個點(B)結束，因此，可以視為這兩個點之中，有可能存在A點連出的的(C)點與B點連出的(D)點，來形成連線。

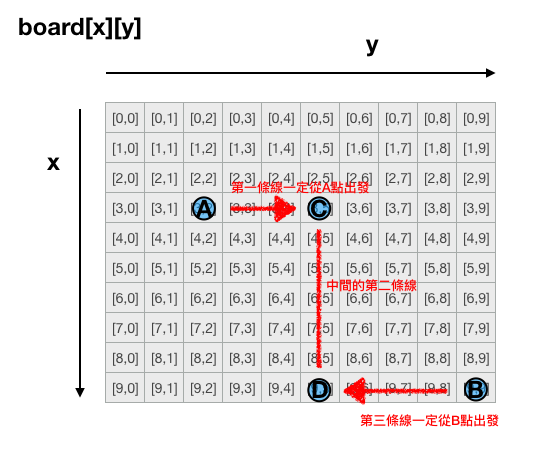
由上圖我們可以觀察出，A點連出的的(C)點絕對是和開始的(A)點在同一行或同一列，B點連出的(D)點絕對是和結束的點(B)點在同一行或同一列。

尋找可能的線的模型

首先，我們來畫出所有有可能連出來的線圖形狀，再來思考該如何去撰寫消除邏輯。

判斷是否存在此圖形的連線

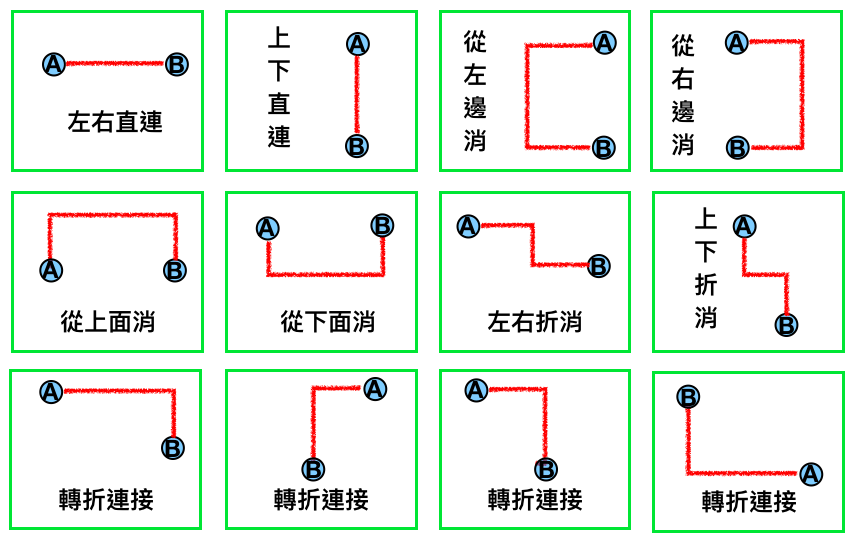
從上面的圖型我們先來分析向左、上、下、右的邊消的情況，要如何去搜尋可能存在的路徑。

讓我們先看這張圖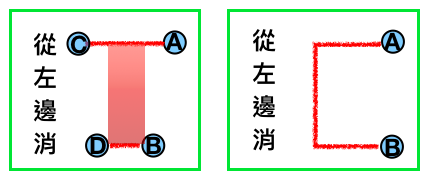

圖中的(A)為起始點，(B)為終點，(C)為(A)點最左能走到的點，(D)為(B)點最左能走到的點。則淡紅色漸層的部份，就是存在著可能的路徑。

這個可能連線的區塊的座標應為: 左上(A.x,D.y)、右上(A.x, B.y)、右下(D.x,D.y)、左下(B.x,B.y)。

我們應該要取A_C與B_D的橫向座標(y)中，有交集的部份。

因此這部份的邏輯程式應為

let potinC = getPathLeftPoint(pointA);
let pointD = getPathLeftPoint(pointB);
let min = Math.max(pointC.y,pointD.y);
let max = Math.min(pointA.y, pointB.y);
for (var i = max;i>=min;i--) {
    if (!hasMiddleValue(new Point(pointA.x, i), new Point(pointB.x, i))) {
        path = [pointA, new Point(pointA.x, i), new Point(pointB.x, i), pointB];
        return "可消除";
    }       
}

同樣的模型可以套用在向左、向上、向右、向下。
我們可以發現，左右直連可視為A點與C點相疊、B點與D點相疊的向上/向下消除，上下直連亦同。轉折連接可視為A與C或者B與D其中有兩個相疊，另兩個不相疊。都可以用相同的演算法來找出路徑

無法用相同的方式找出來的圖形有這兩個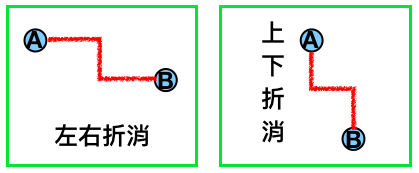

先來繪製出有可能可以連線的區域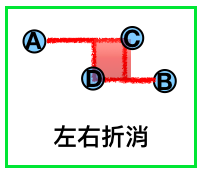

由上圖可知，我們需要找A、B點之間在左邊的(A)點往右可走最多的那個(C)點，然後找A、B點之間在右邊的(B)點往左走最多的(D)點。

然後取出A_C與B_D中y有交集的地方，為有可能可以連線的區域

這部份的邏輯程式碼為

if (pointA.y != pointB.y){
    let leftPoint = (pointA.y < pointB.y) ? pointA:pointB;
    let rightPoint = (pointA.y >= pointB.y) ? pointA:pointB;
    let leftPointRIGHT = getPathRightPoint(leftPoint);
    let rightPointLEFT = getPathLeftPoint(rightPoint);
    leftPointRIGHT.y = (leftPointRIGHT.y < rightPoint.y) ? leftPointRIGHT.y : rightPoint.y;
    rightPointLEFT.y = (rightPointLEFT.y > leftPoint.y) ? rightPointLEFT.y : leftPoint.y;
    if (leftPointRIGHT.y != leftPoint.y && rightPointLEFT.y != rightPoint.y){
        for (var i = rightPointLEFT.y; i <= leftPointRIGHT.y; i++) {
            if (!this.board.hasMiddleValue(new Point(leftPoint.x, i), new Point(rightPoint.x, i))) {
                this.path_Detail = [leftPoint, new Point(leftPoint.x, i), new Point(rightPoint.x, i), rightPoint];
                console.log("same left to right");
                return true;
            }
        }
    }
}